Walker

Image

Time-integrator for stochastic differential equations

Walker is a numerical integrator for stochastic differential equations (SDE). It can be used to analyze and design the evolution of fluctuating variables and their statistics in state space and time. Walker can compute time evolutions of multiple variables governed by coupled SDE systems of different types. It allows the estimation of arbitrary coupled statistics and probability density functions.

In a nutshell, walker solves the Fokker-Planck equation

\[ \newcommand{\bv}[1]{{\mbox{\boldmath$#1$}}} \frac{\partial}{\partial t}F(\bv{Y},t) = - \sum_{\alpha=1}^N \frac{\partial}{\partial Y_\alpha}\big[ A_\alpha(\bv{Y},t) F(\bv{Y},t) \big] + \frac{1}{2} \sum_{\alpha=1}^N \sum_{\beta=1}^N \frac{\partial^2}{\partial Y_\alpha \partial Y_\beta}\big[B_{\alpha\beta}(\bv{Y},t)F(\bv{Y},t)\big] \]
\[ \newcommand{\bv}[1]{{\mbox{\boldmath$#1$}}} \begin{split} \frac{\partial}{\partial t}F(\bv{Y},t) = - \sum_{\alpha=1}^N \frac{\partial}{\partial Y_\alpha}\big[ A_\alpha(\bv{Y},t) F(\bv{Y},t) \big] \\ + \frac{1}{2} \sum_{\alpha=1}^N \sum_{\beta=1}^N \frac{\partial^2}{\partial Y_\alpha \partial Y_\beta}\big[B_{\alpha\beta}(\bv{Y},t)F(\bv{Y},t)\big] \end{split} \]

which is equivalent to the system of SDEs

\[ \newcommand{\bv}[1]{{\mbox{\boldmath$#1$}}} \mathrm{d}Y_\alpha(t) = A_\alpha(\bv{Y},t)\mathrm{d}t + \sum_{\beta=1}^N b_{\alpha\beta}(\bv{Y},t)\mathrm{d}W_\beta(t), \qquad \alpha = 1,\dots,N, \qquad B_{\alpha\beta} = b_{\alpha\gamma}b_{\gamma\beta} \]
\[ \newcommand{\bv}[1]{{\mbox{\boldmath$#1$}}} \begin{split} \mathrm{d}Y_\alpha(t) = A_\alpha(\bv{Y},t)\mathrm{d}t + \sum_{\beta=1}^N b_{\alpha\beta}(\bv{Y},t)\mathrm{d}W_\beta(t), \\ \alpha = 1,\dots,N, \qquad B_{\alpha\beta} = b_{\alpha\gamma}b_{\gamma\beta} \end{split} \]

Here $\mathrm{d}{\mbox{\boldmath$W$}}(t)$ is a vector-valued isotropic Wiener process and $F({\mbox{\boldmath$Y$}},t)$ is the joint probability distribution of $N$ variables $Y_\alpha$ of the sample space. The drift, $A_\alpha$ , and diffusion, $B_{\alpha\beta}$ , functions can be defined in any way as long as the diffusion is positive semi-definite. Walker discretizes and numerically solves the system of SDEs using a large number of particles and can estimate arbitrary statistics and distributions as they evolve in time.

Walker can be used to design statistical moment approximations. If the approximate shape of the probability distribution for a fluctuating variable is known (or can be usefully assumed), its governing SDE can, in some cases, be derived. Numerically integrating this governing equation, Walker allows extracting arbitrary statistics which can be used to test and verify hypotheses of functional forms of statistics as a function of other statistics. This enables, e.g., developing statistical moment approximations for turbulent flows where higher order statistics must be expressed in terms of lower order statistics based on some approximation.

Walker can also be used to design approximations for probability density functions of fluctuating variables. If reasonable assumptions on probability distributions of some key variables of a process can be made, Walker can be used to integrate their governing equations and design parameterizations of those governing equations based on statistics extracted from the computed distributions.

Performance

Walker uses the Charm++ runtime system to run concurrently either on a single machine or a networked set of computers. The software design is asynchronous, yielding 100% CPU utilization at all times, and it exhibits 100% efficiency weak scaling with up to 3 trillion ( $3\!\times\!10^{12}$ ) particles up to 24K CPU cores, see also d5304e78.

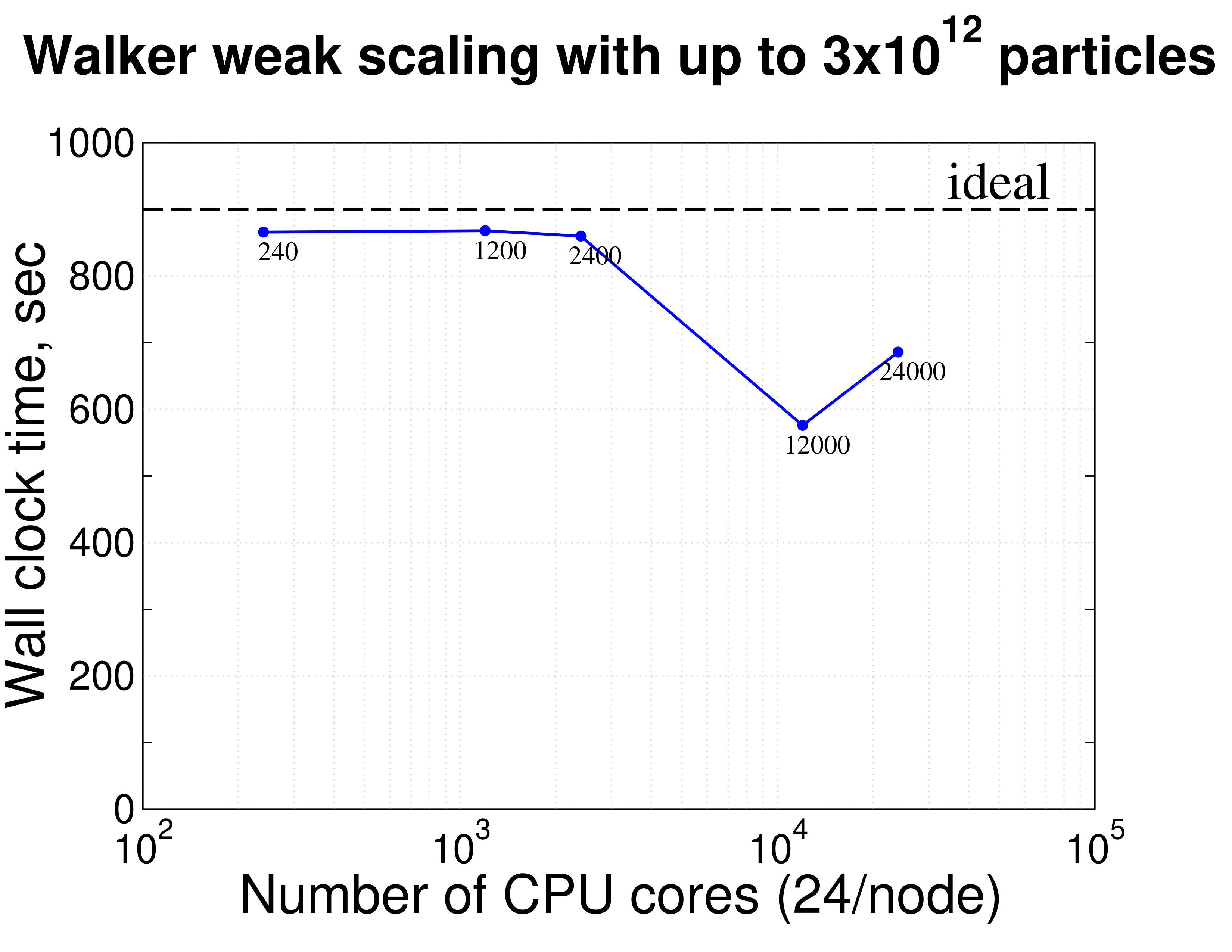Image This figure quantifies the excellent scalability of walker, integrating up to 3 trillion particles and aggregating data across all CPUs for estimating various statistics and probability distributions.

Differential equations

The following differential equations are implemented:

  1. Beta — A system of SDEs, with linear drift and quadratic diagonal diffusion, whose invariant is the joint beta distribution. For more details on the beta SDE, see Bakosi, Ristorcelli, Exploring the beta distribution in variable-density turbulent mixing, J. Turbul, 2010.
  2. Diagonal Ornstein-Uhlenbeck — A system of SDEs with linear drift and constant diagonal diffusion, whose invariant is the joint normal distribution.
  3. Ornstein-Uhlenbeck — A system of SDEs with linear drift and constant diffusion, whose invariant is the joint normal distribution.
  4. Dirichlet — A system of SDEs, whose invariant is the Dirichlet distribution. For more details on the Dirichlet SDE, see Bakosi, Ristorcelli, A Stochastic Diffusion Process for the Dirichlet Distribution, Int. J. Stoch. Anal., 2013.
  5. Generalized Dirichlet — A system of SDEs, whose invariant is Lochner's generalized Dirichlet distribution. For more details on the generalized Dirichlet SDE, see Bakosi, Ristorcelli, A Stochastic Diffusion Process for Lochner's generalized Dirichlet distribution, J. Math. Phys., 2013.
  6. Gamma — A system of SDEs, with linear drift and linear diagonal diffusion, whose invariant is the joint gamma distribution.
  7. Skew-normal — A system of SDEs, whose invariant is the joint skew-normal distribution. For more details on the skew-normal distribution, see Azzalini, Dalla Valle, The Multivariate Skew-Normal Distribution.
  8. Wright-Fisher — A system of SDEs, whose invariant is the Dirichlet distribution. For more details on the Wright-Fisher SDE, see Steinrucken, et al., An explicit transition density expansion for a multi-allelic Wright–Fisher diffusion with general diploid selection, Theor. Popul. Biol., 2013.
  9. Number-fraction beta — A system of SDEs, with linear drift and quadratic diagonal diffusion, whose invariant is the joint beta distribution. The number-fraction beta SDE is based on the beta SDE, additionally computing two more stochastic variables that are functions of the beta variables integrated, assuming that the beta variables are number, or mole-, fractions. For more details on the beta SDE, see Bakosi, Ristorcelli, Exploring the beta distribution in variable-density turbulent mixing, J. Turbul, 2010.
  10. Mass-fraction beta — A system of SDEs, with linear drift and quadratic diagonal diffusion, whose invariant is the joint beta distribution. The mass-fraction beta SDE is based on the beta SDE, additionally computing two more stochastic variables that are functions of the beta variables integrated, assuming that the beta variables are mass-fractions. For more details on the beta SDE, see Bakosi, Ristorcelli, Exploring the beta distribution in variable-density turbulent mixing, J. Turbul, 2010.
  11. Mix number-fraction beta — A system of SDEs, with linear drift and quadratic diagonal diffusion, whose invariant is the joint beta distribution. The mix number-fraction beta SDE is based on the beta SDE, with the following differences: (1) the SDE coefficients are specified consistent with the binary turbulent mixing process, and (2) additionally computing two more stochastic variables that are functions of the beta variables integrated, assuming that the beta variables are number, or mole-, fractions. For more details on the beta SDE, see Bakosi, Ristorcelli, Exploring the beta distribution in variable-density turbulent mixing, J. Turbul, 2010.
  12. Mix mass-fraction beta — A system of SDEs, with linear drift and quadratic diagonal diffusion, whose invariant is the joint beta distribution. The mix mass-fraction beta SDE is based on the beta SDE, with the following differences: (1) the SDE coefficients are specified consistent with the binary turbulent mixing process, and (2) additionally computing two more stochastic variables that are functions of the beta variables integrated, assuming that the beta variables are mass-fractions. For more details on the beta SDE, see Bakosi, Ristorcelli, Exploring the beta distribution in variable-density turbulent mixing, J. Turbul, 2010.

Related pages